How to Build a Library Management System with Harperdb, Ejs and Nodejs

Record management strategies help maintain firms efficiency and productivity. However, without a thorough, documented records management strategy, organizations experience misunderstandings and data loss.

I've seen multiple examples of record mismanagement wreaking havoc on research, as I discovered in my final year of high school when I had to put in a lot of effort to locate books in the library and determine whether or not they existed.

In this article, you will learn how to create a library management system with HarperDB for storage, Ejs for the view, and NodeJs server.

Let's talk about HarperDB, but first, you can check out the Library Management System application in action.

What is HarperDB?

HarperDB is a simple database solution for collecting, disseminating, and analyzing data across your organization. For every data use case your organization and project demand, it provides unrivalled flexibility, speed, security, and value.

Why HarperDB?

HarperDB allows you to run your database everywhere, from the edge to the cloud and everywhere in between.
Support for running complicated, fast, ACID-compliant SQL queries on JSON without duplicating data.
A simple REST API allows for seamless integration into any project or tool. It also supports a variety of languages through various drivers and plugins.
HarperDB Studio has a simple and straightforward management interface that allows you to browse, query, and manage data all in one location without having to code.

Now let us create a HarperDB cloud instance which we will use to connect our application to the database.

Creating HarperDB Cloud Instance

For Library Management System, we'll need to set up a database. If you haven't already done so, go to HarperDB's website create an account.

Click Create New HarperDB Cloud Instance on the dashboard, as seen in the figure below.

Create

After that, choose a database instance type. It can be deployed locally by the user or set up and administered on HarperDB servers (cloud instance). We'll be using the cloud instance in this lesson.

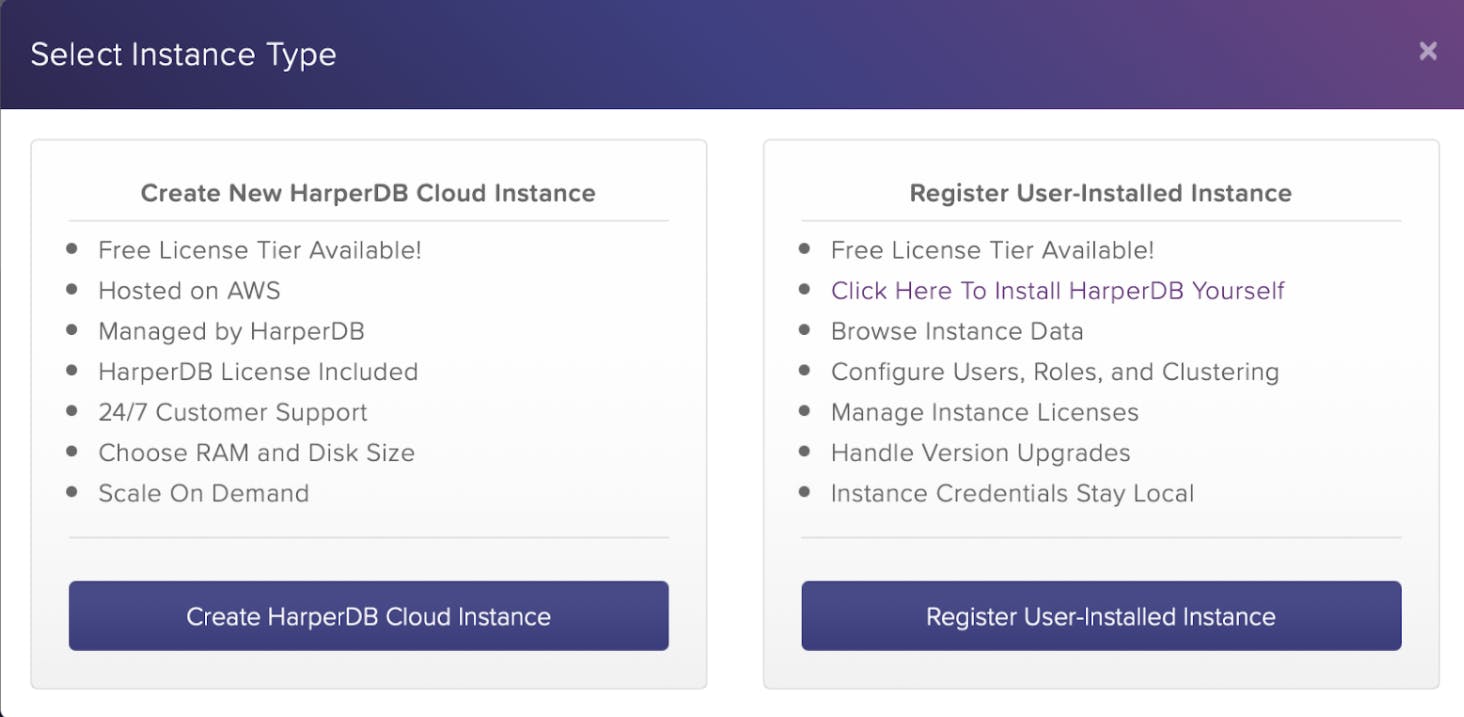
Cloud Instance

You'll have to give details about your cloud instance as shown below, then click the Instance Details button.

Remember to write down your username and password because we'll need them later in the lesson.

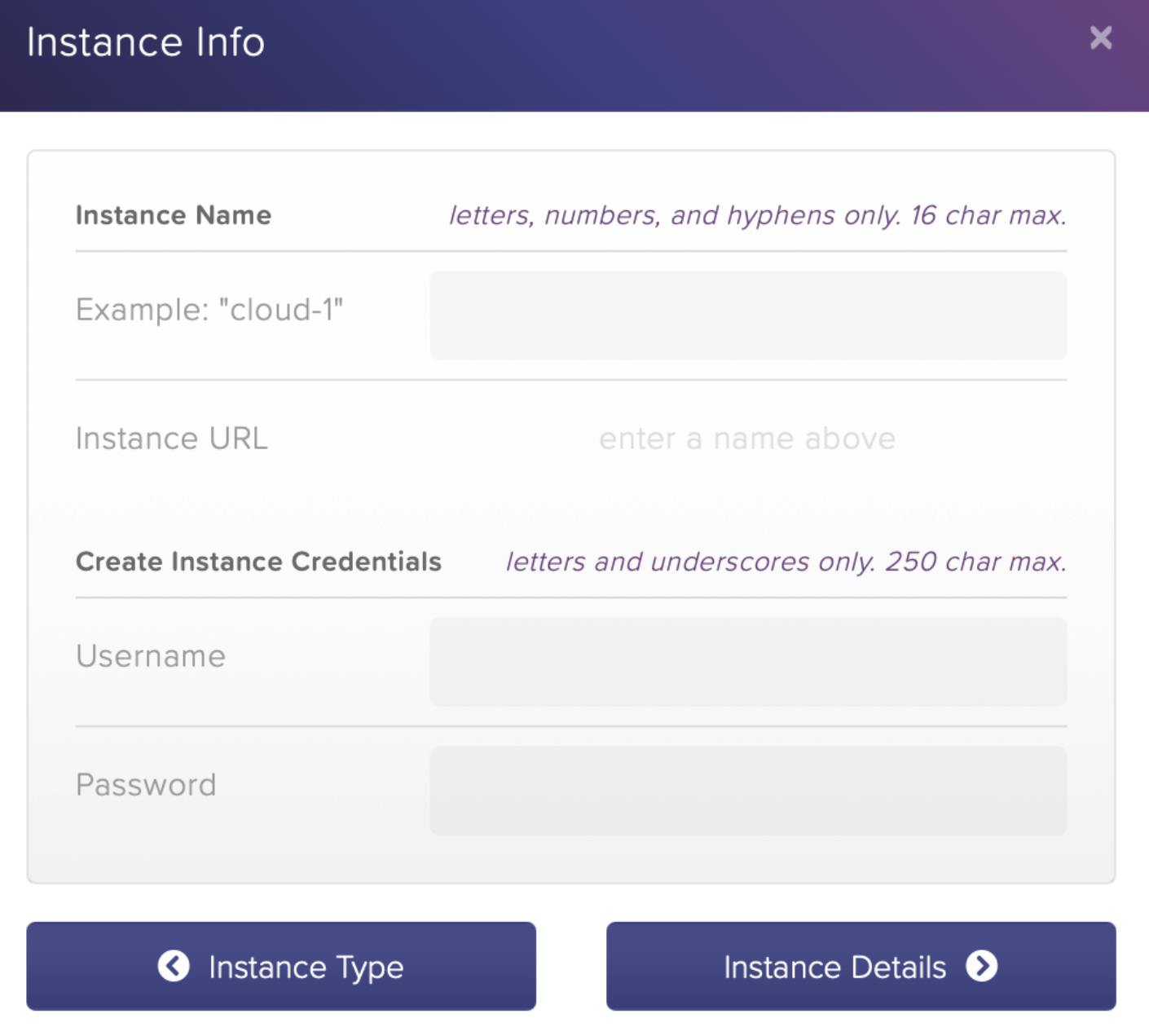
Instance Details

You'll also need to specify the cloud instance's specifications. For example, HarperDB lets you select the amount of RAM, storage size, and region for your model.

Click the Confirm Instance Details button when you've completed all of the configuration details for the cloud instance, and then finish everything to create it.

Note: It takes several minutes to create a cloud instance. Throughout this operation, you will be required to wait. HarperDB also sends out email notifications when an instance is created.

Creating HarperDB Database Schema and Table

Let's create the database schema we'll need for our application. In HarperDB, a schema is a collection of tables, similar to a database in SQL.

Instance Success

To make a schema, go to your dashboard, select the cloud instance, go to the schemas area on the left, and give it a name. We'll use the name book in this example, as shown in the image below:

Create Schema

Let's create Schema Table.

To create a table, go to the table's area on the left side of your dashboard and give it a name and a hash attribute. A hash attribute is similar to Primary Keys in relational databases in that it uniquely identifies each entry in the database.

As seen in the figure below, we'll set the name to record and the hash attribute to record_id.

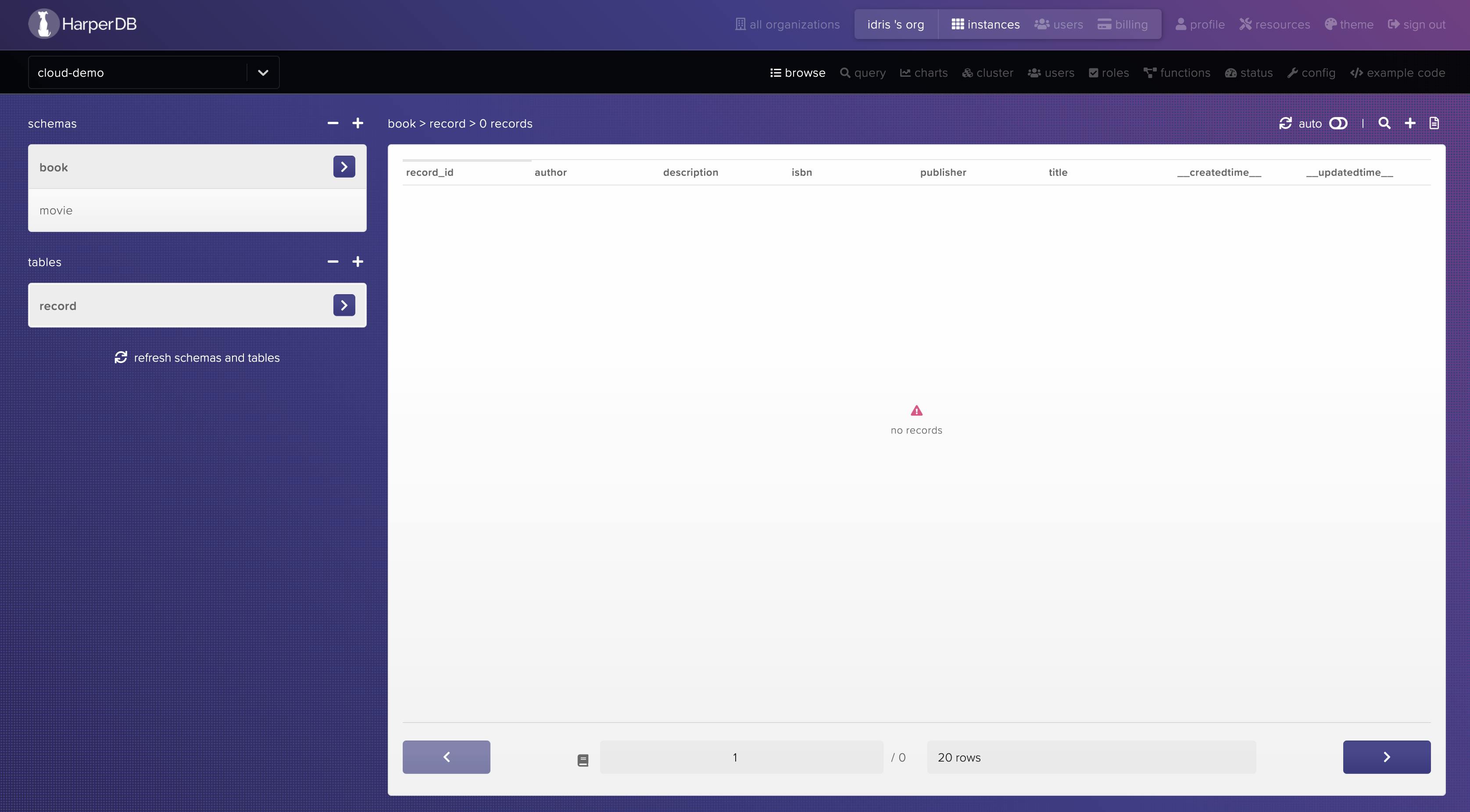
HarperDB Table

Alright, we are done with the Cloud instance and Database setup. Let's proceed to build our application.

Building our Application

I've created the user interface for the Library management system that we'll use in this post for your convenience. To get started, clone this Repository and run the following commands to initialize the app:

git clone https://github.com/Olanetsoft/LMS

cd LMS

We need to install dependencies using this command:

npm install

Note: we need to create a .env file in the root directory and include the following:

PORT=3000

INSTANCE_URL=<your instance URL>
INSTANCE_USERNAME=<your username>
INSTANCE_PASSWORD=<your password>

Ensure to replace <your instance URL> with your instance URL, <your username> with your username and <your password> with your password, which is the credentials we used to create our cloud instance earlier

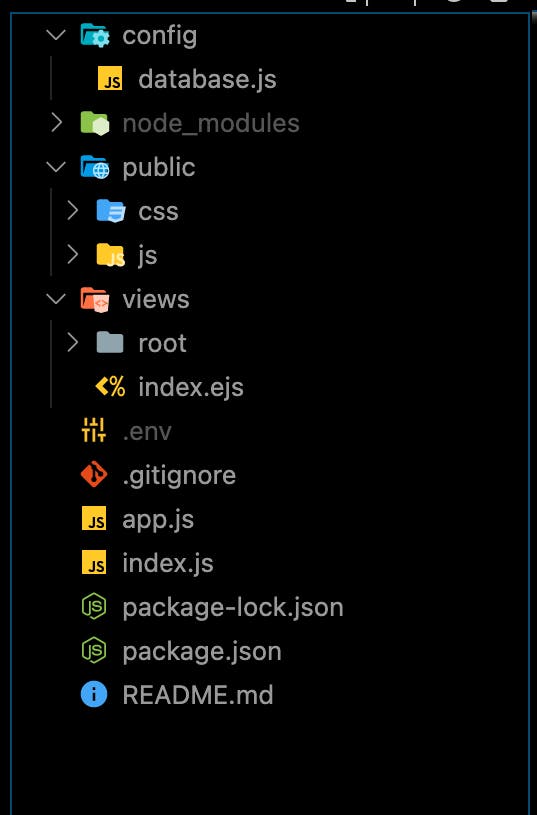
Our Project directory should look similar to what we have below:

Project directory

Let's start our application using the command npm run dev, you should see something similar to what we have below on your browser via http:localhost://3000

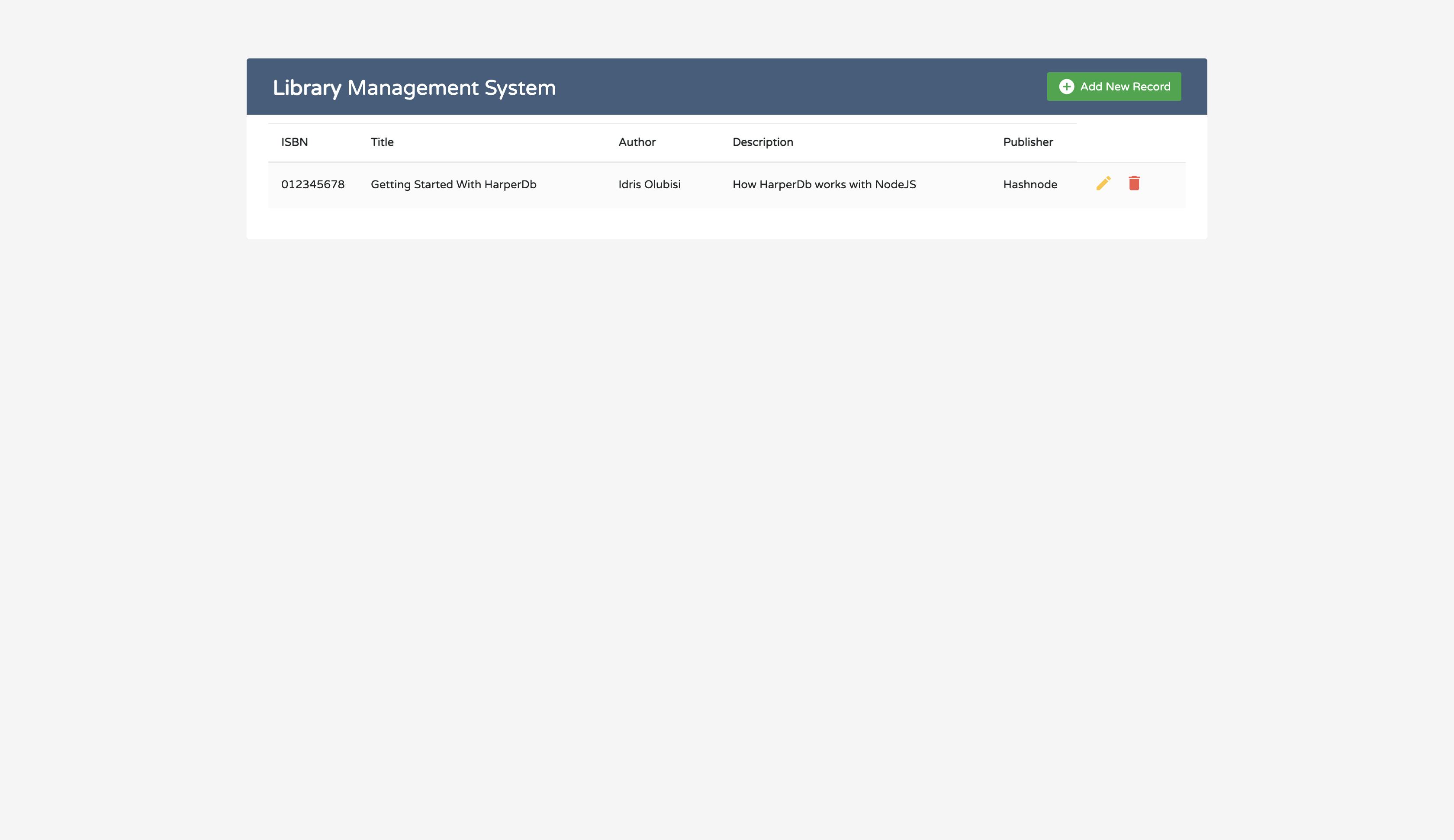
Localhost

Please note that the table's default static record demonstrates how data will be shown when a new one is added.

By running the command npm install we ran earlier, we have installed the dependencies harperive dotenv ejs express and nodemon, which is a development dependency for restarting our server when required:

harperive is a node.js driver for HarperDb.
dotenv is a zero-dependency module that loads environment variables from a .env file into process.env.
ejs is an embedded JavaScript template.

Finally, Express is a fast, unopinionated, minimalist web framework for node.

Project Structure

Let us go through the whole directory before we start writing codes to build our application.

config/database.js - This contains the code implementation that helps to connect to our database in the cloud instance.

public/css - This contains the CSS files we will use in our project.

public/js - This contains the javascript files we are to use in our project

views/root/head - This includes a meta tag and style referencing, which will be reusable across the application.

views/root/end - This includes reference to the script in the public/js directory.

views/index.ejs - This is the landing page of our application.

app.js - This is where we will update by implementing some logic to handle processes in our application.

index.js - This file is where we successfully create our NodeJs server.

Creating New Document and Retrieving all Records in HarperDB

We need to execute an INSERT query in the database via the haperive drive we installed earlier to create new documents in our HarperDB schema. HarperDB offers two options for doing so:

The NoSQL method entails inserting data into the database using the DB context.
The SQL method entails inserting data into the database using a SQL query.

We will be using the NoSQL method in this article.

Kindly navigate to app.js and update it with the snippet below immediately after the "/" route.

// ...

// Add new boook
app.post("/book/add", (req, res) => {

// Get the user data from the request
  const { body } = req;

// Insert a new record into the database
  db.insert(
    {
      operation: "insert",
      schema: "book",
      table: "record",
      records: [body],
    },
    (err, response) => {

// Return, if there is any error
      if (err) {
        return res.status(500).json(err);
      }
// After creating a new record successfully, redirect back to homepage
      res.redirect(302, "/");
    }
  );
});

// ...

Now let us update index.ejs under the to grab user data from the frontend with the snippet below:

<!-- Add Modal HTML -->
<div id="addBookModal" class="modal fade">
   <div class="modal-dialog">
      <div class="modal-content">
         <form action="/book/add" method="POST">
            <div class="modal-header">                        
               <h4 class="modal-title">Add Book Details</h4>
                  <button type="button" class="close" data-dismiss="modal" aria-hidden="true">&times;</button>
             </div>
        <div class="modal-body">                    
           <div class="form-group">
              <label for="isbn">ISBN</label>
                 <input type="text" class="form-control" name="isbn" required>
            </div>
            <div class="form-group">
               <label for="title">Title</label>
                 <input type="text" class="form-control" name="title" required>
            </div>
            <div class="form-group">
               <label for="author">Author</label>
                  <input type="text" class="form-control" name="author" required>
             </div>
             <div class="form-group">
                <label for="description">Description</label>
                  <textarea class="form-control" name="description" required></textarea>
              </div>
              <div class="form-group">
                 <label for="publisher">Publisher</label>
                   <input type="text" class="form-control" name="publisher" required>
               </div>                    
            </div>
            <div class="modal-footer">
               <input type="button" class="btn btn-default" data-dismiss="modal" value="Cancel">
               <input type="submit" class="btn btn-success" value="Add">
              </div>
             </form>
        </div>
    </div>
</div>

On the browser, click on the Add New Record button to enter a new record as shown below:

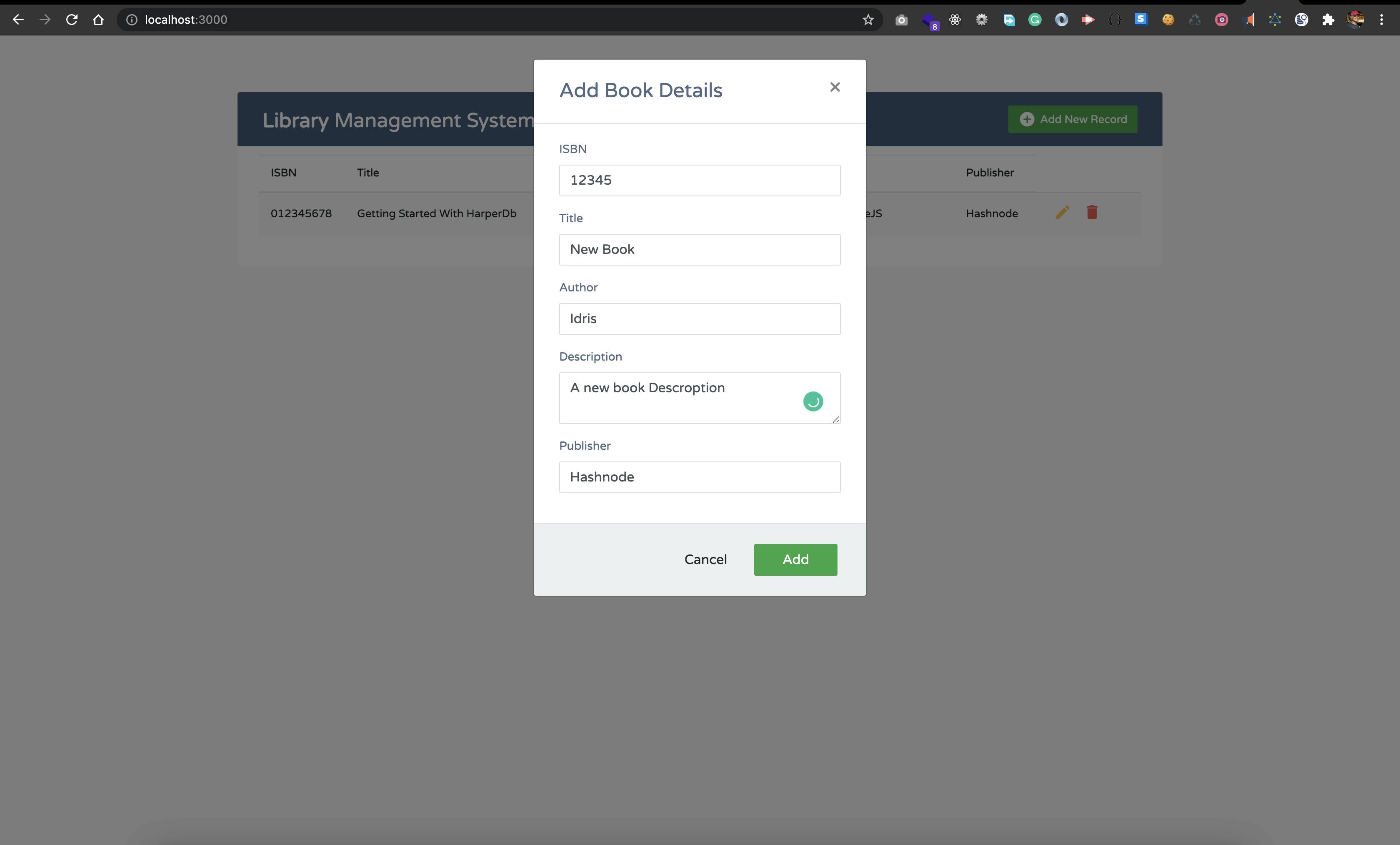
New Record

We have successfully added a new record, but it's not showing on our table. So don't freak out; what we need to do is to pull all the records we have in our database and also update index. ejs.

Let us update the "/" route in the app.js to look like so:

// ...

app.get("/", (req, res) => {
  db.searchByValue(
    {
      operation: "search_by_value",
      schema: "book",
      table: "record",
      searchValue: "*",
      searchAttribute: "record_id",
      attributes: ["*"],
    },
    (err, response) => {
      if (err) {
        return res.status(500).json(err);
      }
      res.render("index", {
        pageTitle: "Home | LMS",
        records: response.data,
      });
    }
  );
});

// ...

Now let's Update the code within the <table></table> tag in index.ejs` to look similar to the snippet below:

// ....

<table class="table table-striped table-hover">
   <thead>
      <tr>
        <th>ISBN</th>
        <th>Title</th>
        <th>Author</th>
        <th>Description</th>
        <th>Publisher</th>
      </tr>
    </thead>
    <tbody>
       <% if (records.length > 0) { %>
           <% for (let rec of records) { %>
              <tr>
                 <td><%= rec.isbn %></td>
                 <td><%= rec.title %></td>
                 <td><%= rec.author %></td>
                 <td><%= rec.description %></td>
                 <td><%= rec.publisher %></td>
                  <td>
       <!-- Edit Modal HTML -->
             <a href="#editBookModal" class="edit" data-toggle="modal"><i class="material-icons" data-toggle="tooltip" title="Edit">&#xE254;</i></a>

               <a href="#deleteBookModal" class="delete" data-toggle="modal"><i class="material-icons" data-toggle="tooltip" title="Delete">&#xE872;</i></a>
                   </td>
                 </tr>
                 <% } %>

                 <% } else { %>
             <tr>
                 <td>012345678</td>
                 <td>Getting Started With HarperDb</td>
                  <td>Idris Olubisi</td>
                  <td>How HarperDb works with NodeJS</td>
                  <td>Hashnode</td>
                  <td>
                      <a href="#" class="edit" data-toggle="modal"><i class="material-icons" data-toggle="tooltip" title="Edit">&#xE254;</i></a>
                       <a href="#" class="delete" data-toggle="modal"><i class="material-icons" data-toggle="tooltip" title="Delete">&#xE872;</i></a>
                  </td>
               </tr>
                   <% } %>
        </tbody>
</table>

// ...

Now we should have something like the image shown below:

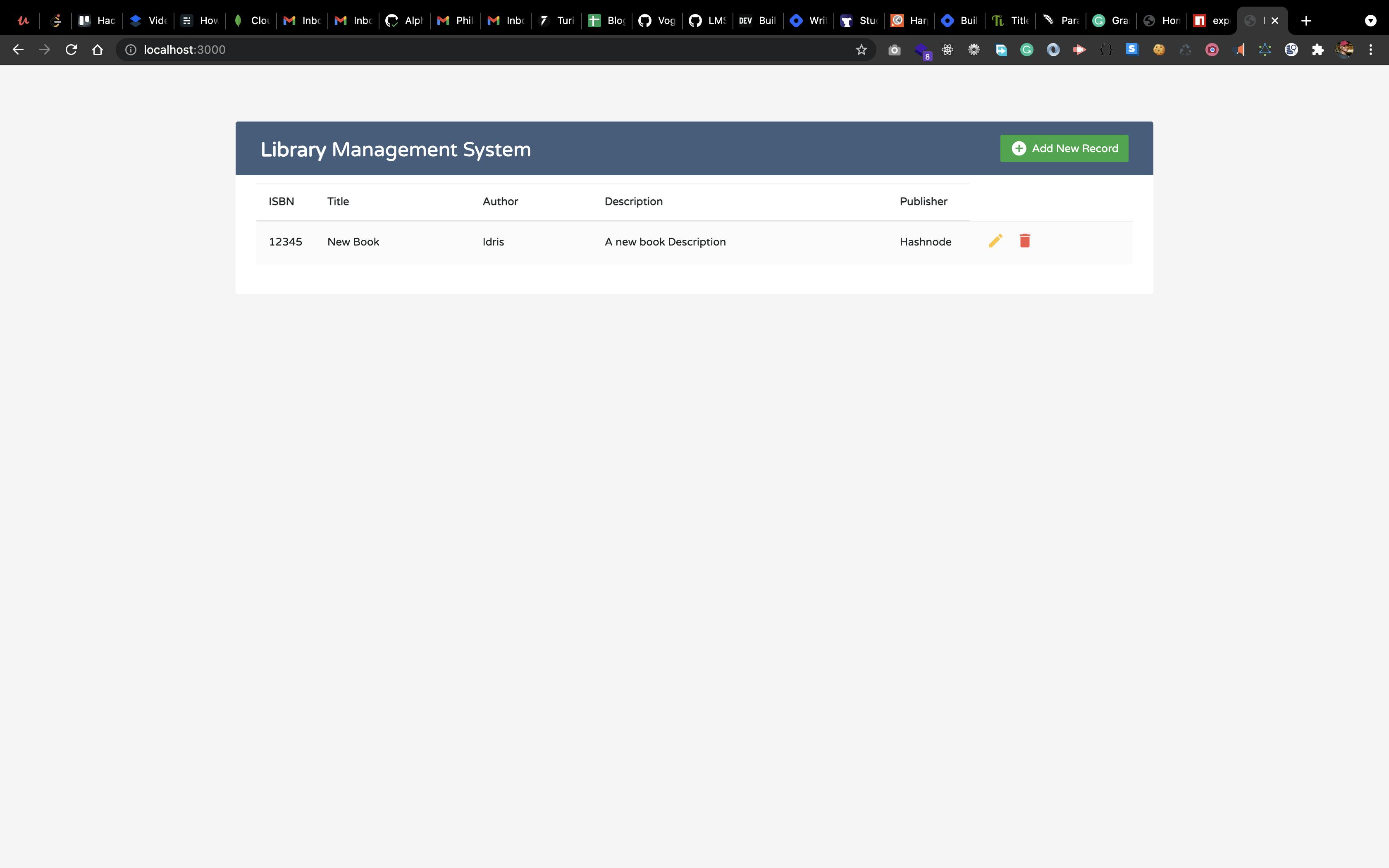
Index.ejs

Yay, 😎 we can now successfully create a new record and also retrieve all records from our database.

Updating and Deleting a Record in HarperDB

To update documents in our HarperDB tables, we will have to use the DB context to execute an UPDATE query in the database and the <!-- Edit Modal HTML -- > section in index. ejs.

To update our record, kindly add the following snippet in app.js immediately after the book/add route.

// ... 

// Updating a record
app.post("/book/edit", (req, res) => {
  const { body } = req;

// Update query
  db.update(
    {
      operation: "update",
      schema: "book",
      table: "record",
      records: [body],
    },
    (err, response) => {
      if (err) {
        return res.status(500).json(err);
      }
// After updating successfully, kindly redirect back to homepage
      res.redirect(302, "/");
    }
  );
});

// ...

Updating index.ejs

<!-- Edit Modal HTML -->
    <div id="editBookModal" class="modal fade">
        <div class="modal-dialog">
           <div class="modal-content">
              <form action="/book/edit" method="POST">
                  <div class="modal-header">                        
                      <h4 class="modal-title">Edit Record</h4>
                       <button type="button" class="close" data-dismiss="modal" aria-hidden="true">&times;</button>
                     </div>
          <div class="modal-body">                    
               <div class="form-group">
                   <label>ISBN</label>
                       <input type="text" class="form-control" name="isbn" value="<%= rec.isbn %>" required>
                </div>
                 <div class="form-group">
                     <label>Title</label>
                          <input type="text" class="form-control" name="title" value="<%= rec.title %>" required>
                 </div>
                 <div class="form-group">
                     <label>Author</label>
                         <input type="text" class="form-control" name="author" value="<%= rec.author %>" required>
                  </div>
                   <div class="form-group">
                        <label>Description</label>
                            <textarea class="form-control" name="description" required><%= rec.description %></textarea>
                    </div>
                     <div class="form-group">
                           <label>Publisher</label>
                                <input type="text" class="form-control" name="publisher" value="<%= rec.publisher %>" required>
                      </div>                    
                         <input type="hidden" class="form-control" name="record_id" value="<%= rec.record_id %>"> 
                      </div>
                       <div class="modal-footer">
                             <input type="button" class="btn btn-default" data-dismiss="modal" value="Cancel">
                               <input type="submit" class="btn btn-info" value="Save">
                            </div>
                      </form>
               </div>
         </div>
</div>

Let's test the update implementation by going to our browser:

Test

Result:

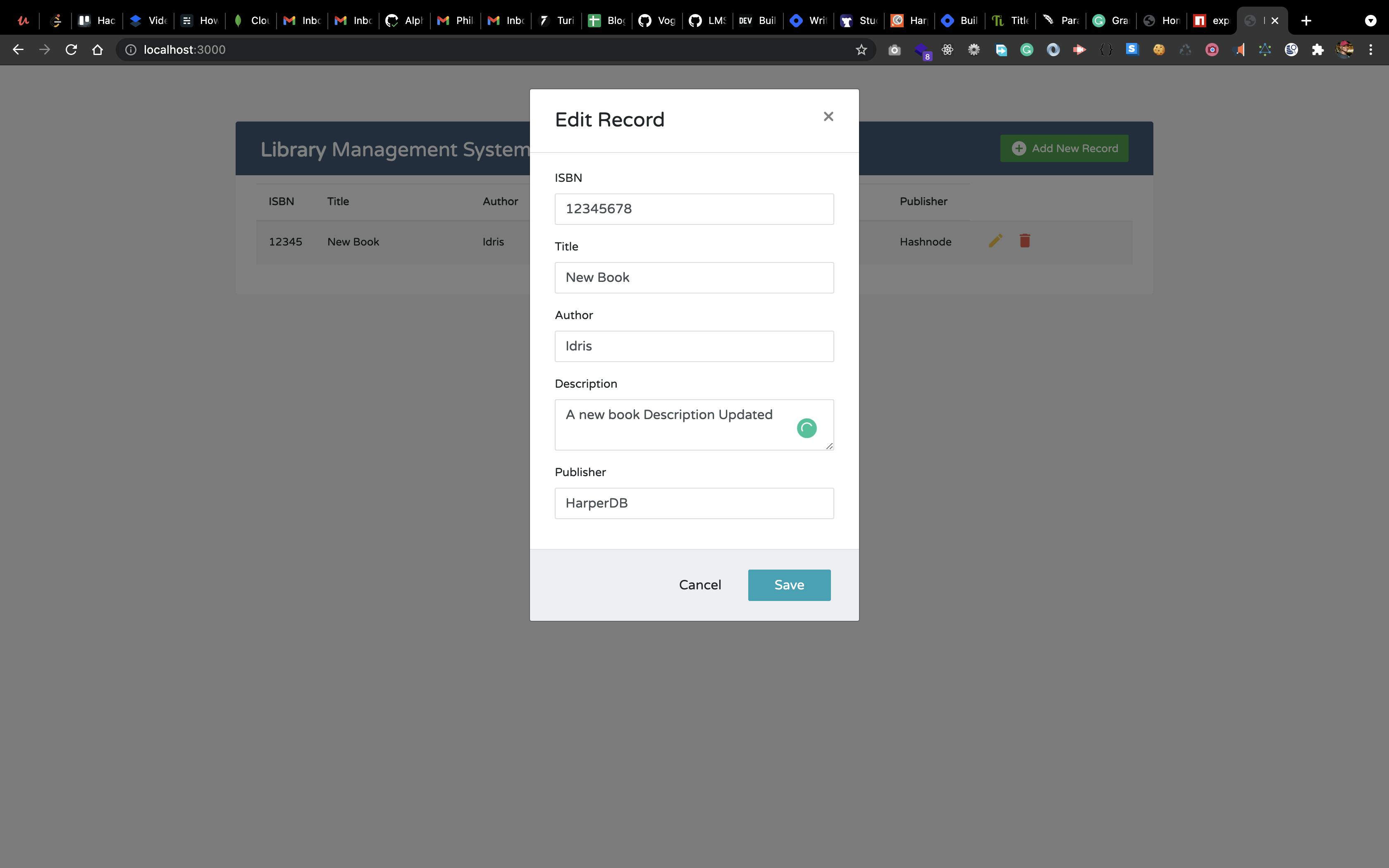
Update Result

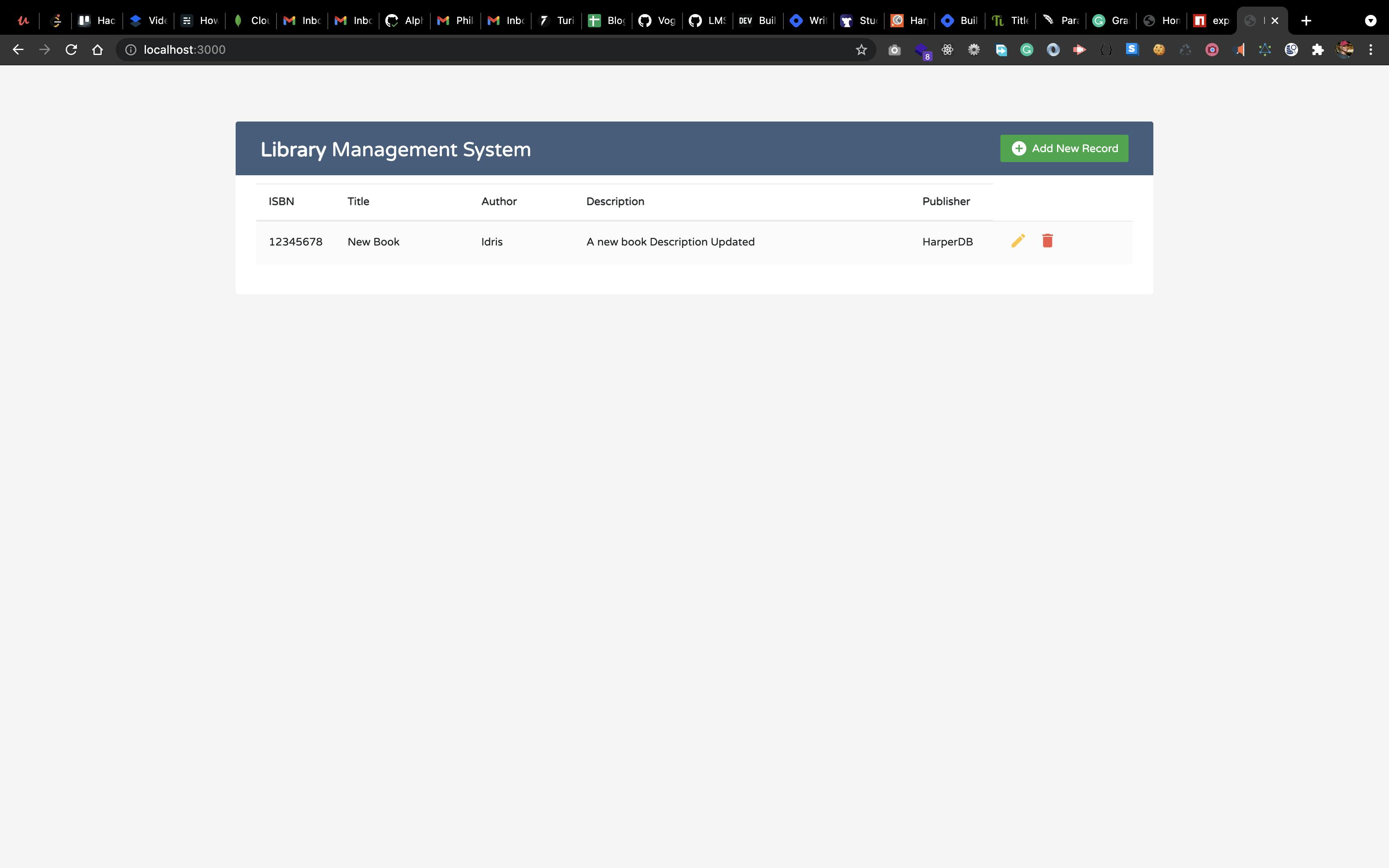
Let's proceed to the delete action by adding the delete implementation in our database and updating  in index.ejs.

Add the following snippet for the delete action in app.js.

// ...

// Delete action
app.post("/book/delete/:record_id", (req, res) => {
  const { record_id } = req.params;

// Delete query
  db.delete(
    {
      operation: "delete",
      schema: "book",
      table: "record",
      hashValues: [record_id],
    },
    (err, response) => {
      if (err) {
        return res.status(500).json(err);
      }

      res.redirect(302, "/");
    }
  );
});

Updating index.ejs

 <!-- Delete Modal HTML -->
 <div id="deleteBookModal" class="modal fade">
     <div class="modal-dialog">
        <div class="modal-content">
           <form action="/book/delete/<%= rec.record_id %>" method="POST">
              <input type="hidden" class="form-control" name="record_id" value="<%= rec.record_id %>"> 
                <div class="modal-header">                        
                   <h4 class="modal-title">Delete Record</h4>
                      <button type="button" class="close" data-dismiss="modal" aria-hidden="true">&times;</button>
                 </div>
                <div class="modal-body">                    
                     <p>Are you sure you want to delete these Records?</p>
                     <p class="text-warning"><small>This action cannot be undone.</small></p>
                </div>
                <div class="modal-footer">
                    <input type="button" class="btn btn-default" data-dismiss="modal" value="Cancel">
                   <input type="submit" class="btn btn-danger" value="Delete">
                 </div>
            </form>
        </div>
   </div>
</div>

Let's Test:

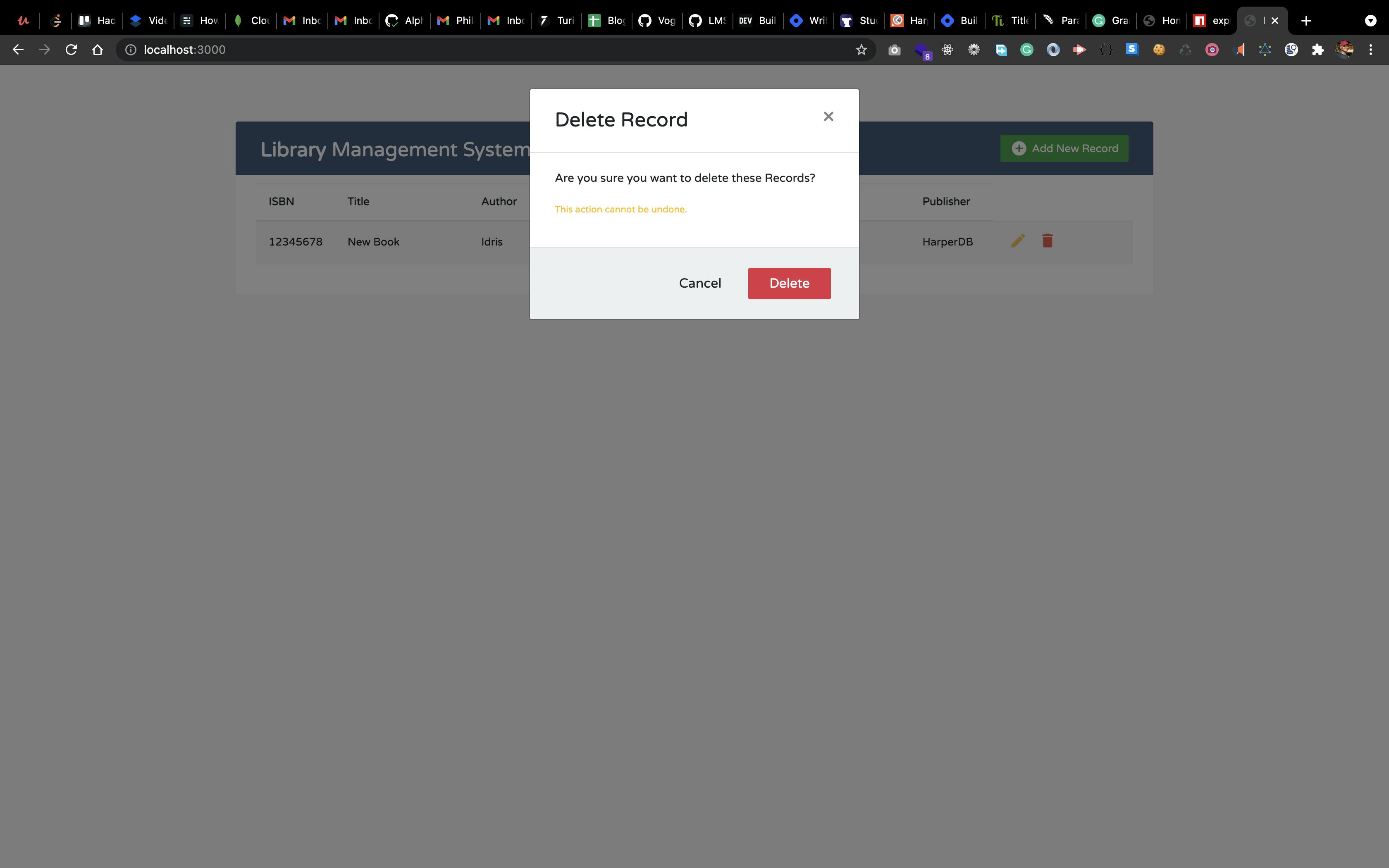
Test Delete

Result:

Delete Result

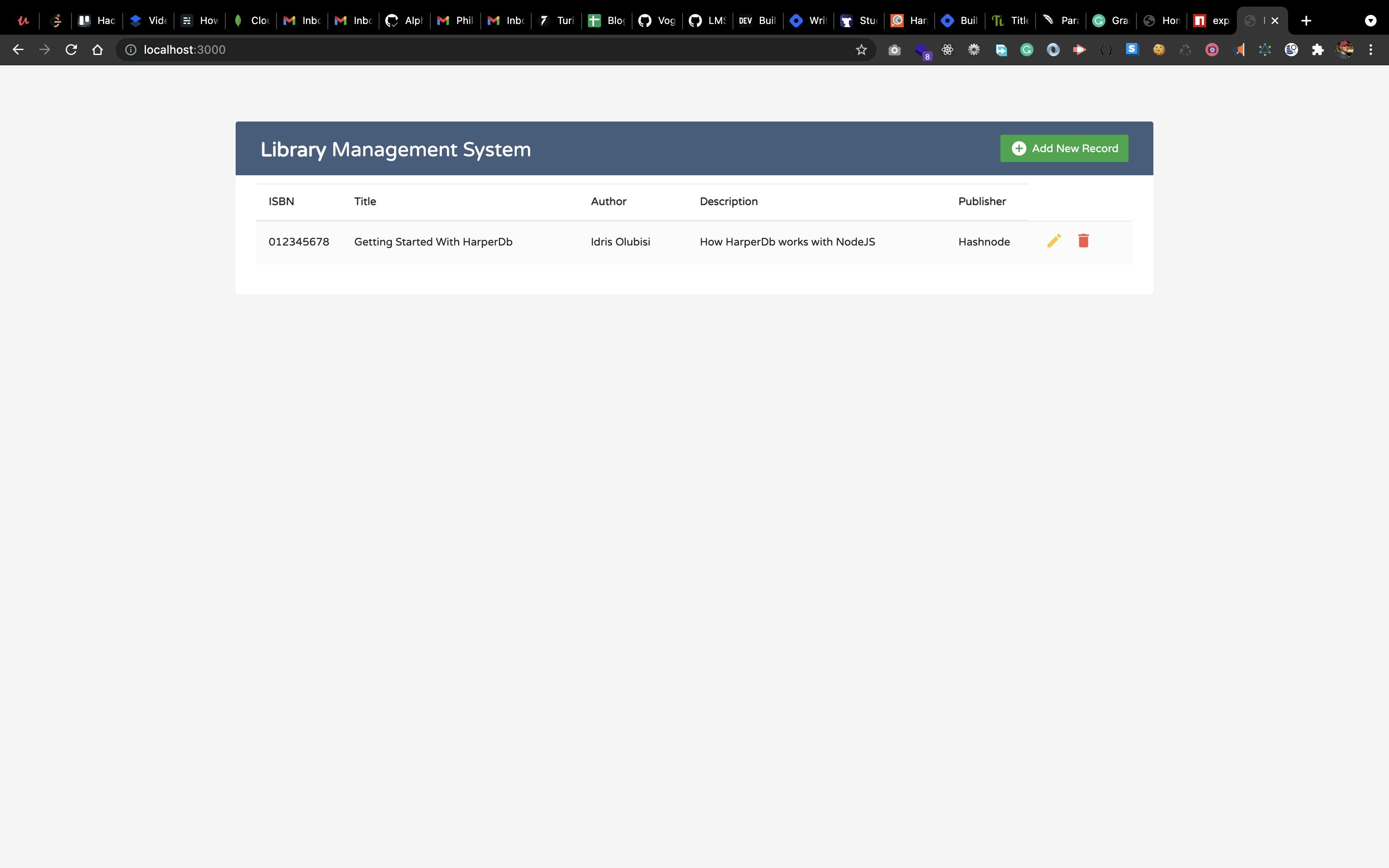
As indicated above, we now have the default static record, meaning that the document has been correctly erased.

Conclusion

We created a library management system with CRUD functionality by integrating HarperDB into our NodeJs. We learned how to use HarperDB to create cloud databases, administer them, and run queries.

The Library Management System's source code is available on GitHub

https://github.com/Olanetsoft/LMS/tree/complete-project

in the complete-project branch.

I'm interested to see what you come up with!

Resources

HarperDB Documentation

Express

Haperive

I'd love to connect with you at Twitter | LinkedIn | GitHub

See you in my next blog article. Take care!!!

How to Build a Library Management System with Harperdb, Ejs and Nodejs

Comments (4)

Tutorials

The Interpretation of Full Stack Development

More from this blog

Building Your First Token: A Solidity Speedrun

Depth Over Trend

How to Set Up Cross-Chain Messaging Between EVM and Cosmos

How Merkle Proofs Work

Celebrating One Year Working on Axelar: Building the Interoperability Future

What is HarperDB?

Why HarperDB?

Creating HarperDB Cloud Instance

Creating HarperDB Database Schema and Table

Building our Application

Project Structure

Creating New Document and Retrieving all Records in HarperDB

Updating and Deleting a Record in HarperDB

Conclusion

Resources

Command Palette

Comments (4)

Tutorials

The Interpretation of Full Stack Development

More from this blog

What is HarperDB?

Why HarperDB?

Creating HarperDB Cloud Instance

Creating HarperDB Database Schema and Table

Building our Application

Project Structure

Creating New Document and Retrieving all Records in HarperDB

Updating and Deleting a Record in HarperDB

Conclusion

Resources